論理ゲートを使ってALU(Arithmetic Logic Unit)を作る

ALU(Arithmetic Logic Unit)とは？

ALUとはCPUの中枢となる演算装置です。

今回は1bitの入力Aと入力Bに対して、以下の処理を行うことのできるALUを作ります。

ALU Operation Function
0000 AND
0001 OR
0010 add
0110 subtract
1100 NOR

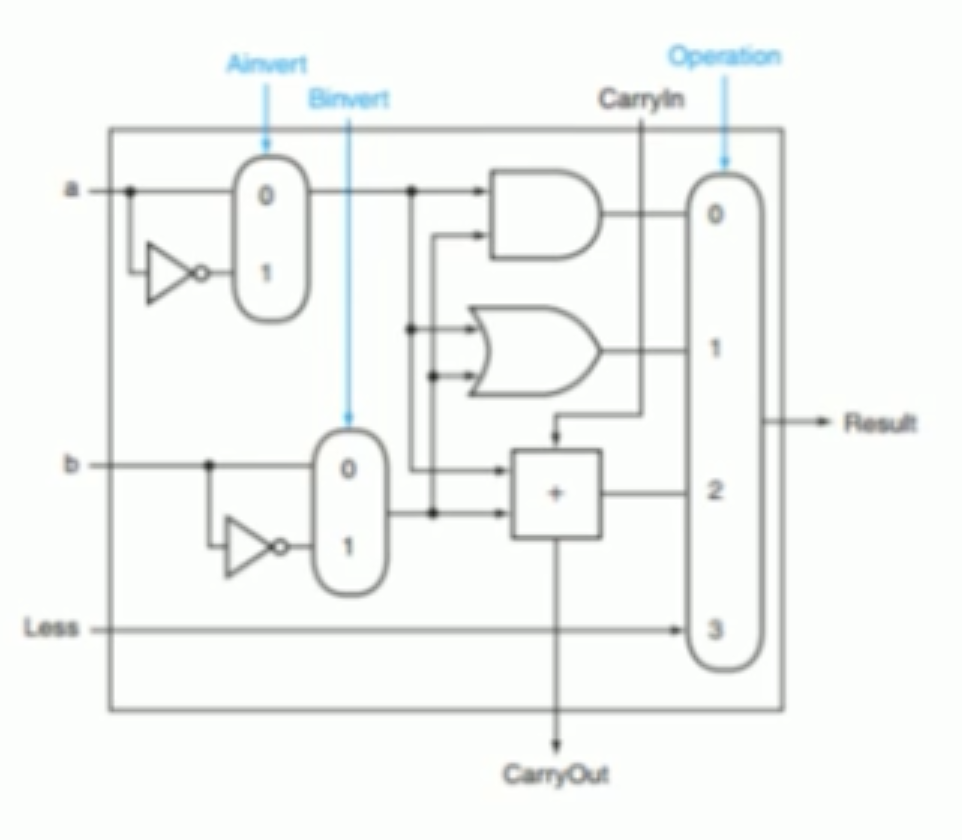
ALUの完成図は以下です。これをPythonで実装します。

ALU

流れ

  1. 論理ゲートを実装する
  2. 全加算器を実装する
  3. Decoderを実装する
  4. Multiplexerを実装する
  5. ALUを実装する

かなり駆け足な説明になります。

1/5. 論理ゲートを実装する

AND, OR, NOT, XORを関数として実装します。

実装

例えばANDだと以下のようになります。

def AND(A, B):
    return A and B

https://github.com/wadayamada/Designing-A-Computer/blob/main/logic_gate.py

2/5. 全加算器を実装する

図と真理値表

全加算器

実装

def full_adder(A, B, C_in):
    Q1 = XOR(A, B)
    Q2 = AND(A, B)
    Q3 = XOR(Q1, C_in)
    Q4 = AND(Q1, C_in)
    Q5 = OR(Q2, Q4)
    S = Q3
    C_out = Q5
    return {"C_out": C_out, "S": S}

https://github.com/wadayamada/Designing-A-Computer/blob/main/adder.py

3/5. Decoderを実装する

図と真理値表

Decoder

Y X Out
0 0 1000
0 1 0100
1 0 0010
1 1 0001

実装

def decoder(Y, X):
    X_not = NOT(X)
    Y_not = NOT(Y)
    Out0 = AND(X_not, Y_not)
    Out1 = AND(X, Y_not)
    Out2 = AND(X_not, Y)
    Out3 = AND(X, Y)
    return Out0, Out1, Out2, Out3

https://github.com/wadayamada/Designing-A-Computer/blob/main/decoder.py

4/5. Multiplexerを実装する

Multiplexerは出力する値をSで選択することができます。

図

Multiplexer

実装

def multiplexer(A, B, S):
    return OR(
        AND(A, NOT(S)),
        AND(B, S)
    )

https://github.com/wadayamada/Designing-A-Computer/blob/main/multiplexer.py

5/5. ALUを実装する

図と真理値表

ALU

A_invert B_invert Operation(Op1, Op0) Function
0 0 00 AND
0 0 01 OR
0 0 10 add
0 1 10 subtract
1 1 00 NOR

AND(0000)

A_invert, B_invertが0なので、A, Bの反転はありません。

Operationが00なので、ANDが選択されます。

OR(0001)

A_invert, B_invertが0なので、A, Bの反転はありません。

Operationが01なので、ORが選択されます。

add(0010)

A_invert, B_invertが0なので、A, Bの反転はありません。

Operationが10なので、addが選択されます。

subtract(0110)

A_invertが0なので、Aの反転はありません。

B_invertが1なので、Bは反転されます。またB_invertは全加算器のC_inに入れます。ですので、結果的に、Bの2の補数が取られます。

Operationが10なので、addが選択されます。

AとBの2の補数のaddなのでA-Bになります。

NOR(1100)

A_invert, B_invertが1なので、A, Bが反転されます。

Operationが00なので、ANDが選択されます。

AND(NOT(A), NOT(B))はド・モルガンの法則より、NOR(A, B)になります。

実装

def ALU(A, B, A_invert, B_invert, Op1, Op0):

    A_selected = multiplexer(A, NOT(A), A_invert)
    B_selected = multiplexer(B, NOT(B), B_invert)

    AND_result = AND(A_selected, B_selected)
    OR_result = OR(A_selected, B_selected)
    ADD_result = full_adder(A_selected, B_selected, B_invert)["S"]
    NOT_USE = 0

    Result = multiplexer4(AND_result, OR_result, ADD_result, NOT_USE, Op1, Op0)

    return Result

https://github.com/wadayamada/Designing-A-Computer/blob/main/ALU.py

参考

The Foundations of Computer Design | Udemy